Le l'onde sonore a deux caractéristiques fondamentale : son amplitude et sa fréquence.
Amplitude
L’amplitude est l’une des caractéristiques principales d’un son. La force perçue dépend, entre autres, de l’amplitude : le son peut être fort ou doux. Dans l’air, l’amplitude correspond aux variations de pression de l’onde.
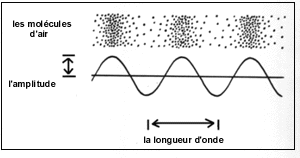
Les vibrations sonores peuvent «comprimer» les molécules d’air très fortement ou très faiblement. Cette compression s’appelle «amplitude» et elle est représentée dans la partie supérieure du schéma ci-dessous. La partie inférieure du schéma illustre la pression de l’air se produisant au cours d’une onde sonore. La ligne horizontale représente la pression d’air normale.
NB : Des ondes sonores ayant la même fréquence peuvent avoir une amplitude différente.
Unité de mesure
Habituellement la pression est mesurée en pascals, mais en acoustique l’amplitude se mesure en décibels (dB), unité qui utilise le logarithme soit du rapport de l’amplitude sonore sur l’amplitude de référence exprimée en watts par mètre carré (W0 = 10-12 W·m-2) :
soit du rapport de la pression produite sur la pression de référence, exprimées en pascals (P0 = 2·10-5 Pa) :
0 dB correspond au minimum que l’oreille humaine peut percevoir appelé seuil d’audibilité, et non au silence absolu . Cette valeur a été choisie par expérimentation pour un son de fréquence 1000 Hz (voir la définition de la fréquence ci-dessous), elle vaut 10-12 W.m-2, mais la plupart des personnes ont un seuil d’audibilité supérieur à 0 dB (environ 4 dB). Le seuil de douleur est de 130 dB, mais l’oreille peut subir des dommages à partir de 85 dB. Il suffit de changer la référence de puissance ou de pression (P0 ou W0 dans les formules ci-dessous) pour que l’échelle des volumes soit complètement changée
Logarithme : explication
Pour une équation du type exponentielle y=ax ,on a x=loga(y) qui se lit : « Logarithme en base a de y » .La fonction logarithmique est la fonction inverse de la fonction exponentielle.
Quelques exemples
103 = 1000, 24 = 16.
Le logarithme de 1000 en base 10 est 3.
Le logarithme de 16 en base 2 est 4.
Le logarithme a été choisi en tant qu’unité car il permet d’avoir des chiffres simples à manipuler, qui ne deviennent pas extrêmement grands, ou petits, et parce que cette approche correspond mieux à ce que perçoit l’oreille humaine en terme de sensation sonore . En revanche, la notion de niveau sonore ne donne qu’une idée vague de la sensation perçue, car la sensibilité de l’oreille doit être prise en compte. Celle-ci varie principalement selon la fréquence du son ; notons que l’oreille est moins sensible aux basses fréquences.
Différentes mesures de l'amplitude
Il existe plusieurs mesures de l’amplitude d’un son, et par extension, d’un signal quelconque de nature ondulatoire :
- L’amplitude moyenne (la valeur moyenne arithmétique du signal positif)
Valeur moyenne =
Cette valeur moyenne est aussi appelée « niveau continu » .
- L’amplitude efficace (amplitude continue équivalente en puissance).
Valeur efficace =
- L’amplitude de crête
Elle correspond à l’amplitude maximale positive.
- L’amplitude de crête à crête (ou cc)
Elle correspond à l’écart maximal d’amplitude positive et négative.
Remarque : La valeur « crête à crête » est égale à la valeur moyenne multipliée par π pour un signal sinusoïdal.
Fréquence
Définition
La fréquence est le nombre de périodes effectuées par un signal en une seconde, c’est-à-dire le nombre de fois par seconde où un même mouvement d’une molécule d’air se reproduit. Si ce mouvement, transmis par l’air à notre tympan, est périodique, nous entendrons un son dont la hauteur sera facilement identifiable. Dans le cas contraire, nous entendrons plutôt un bruit. La fréquence est directement liée à la hauteur d’un son perçu, mais n’en est qu’une des composantes. À une fréquence faible correspond un son grave, à une fréquence élevée un son aigu.
F=T-1 F, fréquence en Hz
T, période en s
La fréquence est mesurée en Hertz (Hz) : 1Hz correspond à une seule vibration complète par seconde (La du diapason = 440 Hz).
Quelques repères
Les fréquences ont ensuite été classées de manière à instaurer un même langage :
En dessous de 20 Hz : inaudible : infrasons
De 20 Hz à 400 Hz : audible : graves
De 400 Hz à 1600 Hz : audible : médiums
De 1600 Hz à 20 KHz : audible : aigus
Au-dessus de 20 KHz : inaudible : ultrasons
L’ensemble des fréquences audibles (20 Hz à 20 KHz) constitue le spectre sonore . Un autre classement purement musical, mais qui s’étend aujourd’hui de plus en plus aux techniques audio, est le regroupement des fréquences par octave (ou demi-octave ou tiers d’octave). Quand une fréquence est doublée ou divisée par 2, on dit qu’elle augmente ou qu’elle diminue d’une octave (20 Hz et 40 Hz, 150 et 300 Hz, 1600 et 800 Hz, etc…).
Une norme décompose à présent le spectre sonore en 10 octaves :
20 à 40 Hz
40 à 80 Hz
80 à 160 Hz
160 à 315 Hz
315 à 630 Hz
630 à 1250 Hz
1,25 à 2,5 KHz
2,5 à 5 KHz
5 à 10 KHz
10 à 20 KHz
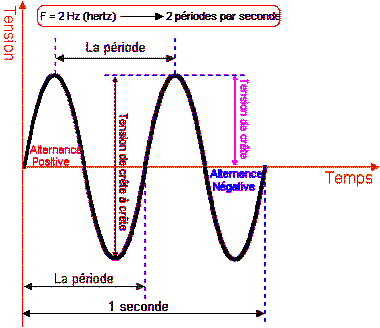
On peut replacer tous ces éléments dans un schéma bilan sur la tension d’un courant alternatif (assimilable à l’amplitude) en fonction du temps analogue à l’onde sonore . On considère alors l’ordonnée zéro comme l’amplitude de référence :