- Modes
fondamental et harmoniques
- Un exemple : L'expérience de Melde
On considère une corde très
fine tendue entre deux points fixes. On suppose que la corde n'est le siège
que de vibrations transversales grâce à un système vibratoire : les points de la corde se déplacent dans
une direction perpendiculaire à celle de la corde immobile. Toute vibration
de la corde pour laquelle chaque point vibre (la position du point en
fonction du temps est une sinusoïde) à la même fréquence est un mode
propre de vibration. La fréquence correspondante est une fréquence propre.
La corde est immobilisée
à ses deux extrémités. Ces conditions ne permettent pas toutes les
fréquences possibles. Elles imposent des modes propres formant une suite
arithmétique.
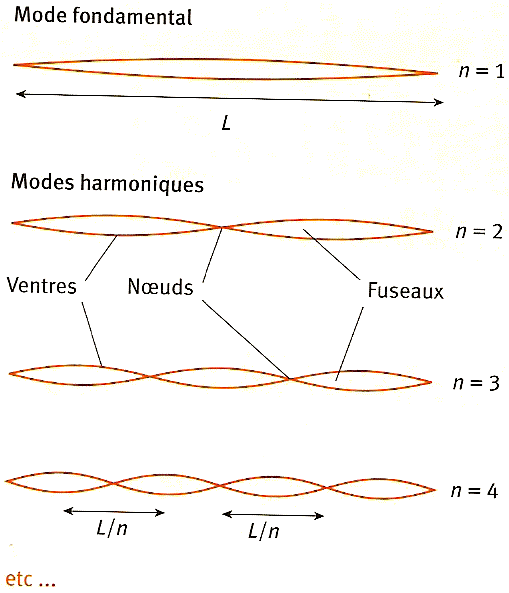 Le mode propre dont la fréquence est la plus basse (n = 1) est
appelé mode fondamental : sa fréquence propre est notée f1.
Le mode propre dont la fréquence est la plus basse (n = 1) est
appelé mode fondamental : sa fréquence propre est notée f1.
Les autres modes
propres sont appelés modes harmoniques. Ils sont caractérisés par
un nombre entier n. La fréquence fn
de l'harmonique n est égale à n fois
la fréquence fondamentale : fn
= n·f1.
Les fréquences
propres sont quantifiées.
Excitons
sinusoïdalement la corde par une force appliquée sur un petit
élément de longueur. Pour qu'elle se mette à vibrer, il est
nécessaire que la fréquence d'excitation soit égale à une de ses
fréquences propres. A cette fréquence, les points de la corde
vibrent sinusoïdalement avec une amplitude qui dépend de leur
position. Lorsqu'ils sont situés à un ventre de vibration,
l'amplitude est maximale et à un nœud de vibration, l'amplitude
est nulle.
Lorsque la corde
vibre selon un de ses modes propres, on remarque la présence de
fuseaux de longueurs égales. L'extrémité d'un fuseau est un nœud
de vibration ; le milieu d'un fuseau est un ventre de vibration.
Pour l'harmonique n, la longueur d'un fuseau est
égale à L/n où L est la longueur de la corde.
Lorsqu'une corde de
piano n'est plus excitée par une force sinusoïdale mais frappée, ses
oscillations libres produisent un son composé de sons sinusoïdaux dont les
fréquences sont celles des modes propres de la corde. La fréquence du son
produit est égal à celle du mode fondamental.
Les vibrations libres de la
corde sont donc une superposition des modes de vibrations propres de la
corde.
On en arrive ainsi à la
définition d'un harmonique :
Deux sons sont dits harmoniques (... et notre oreille les reconnaît en
harmonie) lorsqu'ils vibrent avec des fréquences multiples l'une de l'autre.
C'est-à-dire que l'un est un harmonique de l'autre qui est un fondamental
ou qu'ils ont la même fréquence au quel cas
on les dit à l'unisson.
Mise en
évidence de l'existence de nœuds (et donc de fuseaux) par l'expérience de
la farine
Lorsqu'un son B a une fréquence double
d'un son A, on dit que B est à l'octave de A.
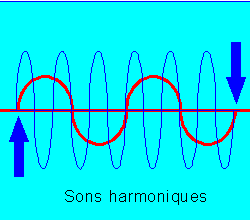 Dans le schéma ci-contre, l'onde jaune est la représentation du son
produit par une note quelconque, disons un La2.
Dans le schéma ci-contre, l'onde jaune est la représentation du son
produit par une note quelconque, disons un La2.
L'onde B en rouge a une fréquence double de la jaune A (deux ondes
rouges pour une jaune). Elle représente le La3, une octave au-dessus
du La2. C'est un harmonique du son A.
L'onde C en bleu a une fréquence encore double de la rouge. Elle représente
le La4, à l'octave du La3.
Un
son n'est jamais pur. Il s'accompagne toujours d'autres sons qui n'ont
pas la même fréquence que lui. Cependant une harmonie peut exister
entre deux sons, même s'ils ne sont pas à l'octave l'un de l'autre.
Il suffit pour cela que leurs ondes se croisent à certains moments et
à intervalles réguliers.
Les
flèches indiquent deux points de croisement sur l'axe de propagation
(Ce sont des nœuds). Cette
rencontre se reproduit périodiquement. Le son en bleu et le son en
rouge sont des harmoniques.
On
appelle dissonance (contraire de la consonance) la rencontre de sons qui ne
s’accordent pas et qui provoquent un effet désagréable dû à leur
succession ou à leur simultanéité. Les sons ainsi entendus donnent une
impression plus ou moins prononcée d’incohérence harmonique.
- Le
spectre fréquentiel d'un signal sonore
 Les premiers travaux de Joseph Fourier sur la décomposition d'une fonction
périodique de forme quelconque en une somme de fonctions sinusoïdales
simples avaient laissé penser que la différence entre deux sons de mêmes
fréquences et amplitudes devait se trouver dans l'analyse harmonique du
son.
Les premiers travaux de Joseph Fourier sur la décomposition d'une fonction
périodique de forme quelconque en une somme de fonctions sinusoïdales
simples avaient laissé penser que la différence entre deux sons de mêmes
fréquences et amplitudes devait se trouver dans l'analyse harmonique du
son.
Une série de Fourier
est une série de fonctions sinusoïdales de fréquences multiples à
une fréquence f, la fréquence fondamentale ou fréquence
du fondamental, dont la somme permet de construire une fonction périodique
déterminée de fréquence f. Chaque terme (fonction
sinusoïdale) de la série est un harmonique de cette fonction périodique.
La fonction sinusoïdale de fréquence fn
est appelée harmonique de rang n. Toute fonction périodique
peut se mettre sous la forme d'une série de Fourier. L'idée de décomposition
en série trigonométrique est apparue à Joseph Fourier pour résoudre
l'équation de la chaleur (mais ça, c'est une autre histoire !).
Une fonction périodique réelle
f de période T, continue et dérivable par
intervalles peut se décomposer en une somme pondérée de fonctions sinusoïdales
simples
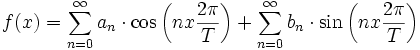
où les coefficients ai et bi
(dits coefficients de Fourier) sont des constantes réelles. Cette décomposition
est aussi appelée « analyse harmonique ».
Pour un entier n
donné, la fonction:
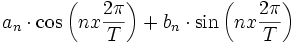
est appelée « harmonique d'ordre n ».
Pour une fonction non périodique,
il existe une généralisation de la série de Fourier nommée transformée
de Fourier. La transformée de Fourier 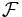 est une opération qui transforme une fonction intégrable en une autre
fonction intégrable. Si ƒ(x) est une fonction intégrable,
sa transformée de Fourier est notée F(s)
est une opération qui transforme une fonction intégrable en une autre
fonction intégrable. Si ƒ(x) est une fonction intégrable,
sa transformée de Fourier est notée F(s)
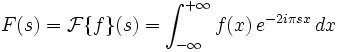
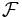 est aussi parfois notée
est aussi parfois notée 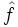 ou TF(ƒ) (Transformée de Fourier de la fonction f).
En physique, la transformation de Fourier permet de déterminer
le spectre d'un signal.
ou TF(ƒ) (Transformée de Fourier de la fonction f).
En physique, la transformation de Fourier permet de déterminer
le spectre d'un signal.
- Intérêt de la transformée de Fourier
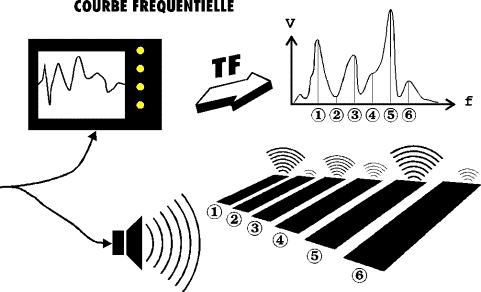
 La TF permet la recherche de composantes périodiques dans un signal.
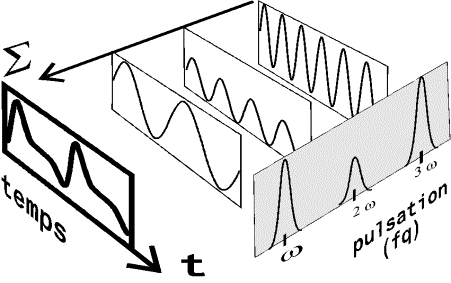
Les signaux
ci-contre sont équivalents. L'un correspond à une série temporelle,
l'autre à son spectre de Fourier.
La TF permet la recherche de composantes périodiques dans un signal.
Les signaux
ci-contre sont équivalents. L'un correspond à une série temporelle,
l'autre à son spectre de Fourier.
La série temporelle (extrait donné en bleu) ne montre rien de définissable.
Son spectre de Fourier dévoile en revanche les fréquences propres
qui constituent le signal, en les distinguant clairement du bruit.
La théorie de Fourier a été étendue, et on est maintenant capable
de décomposer n'importe quel signal (périodique ou non) en une série
de composantes sinusoïdales. Cela signifie que tout son se décompose
en une somme de sons purs.
Les sons périodiques et pseudo-périodiques se décomposent en un
nombre fini de composantes. A l'inverse, les sons apériodiques se décomposent
en un nombre infini de composantes. Cela signifie que lorsqu'on
affiche la représentation spectrale d'un signal (obtenue par
transformation de Fourier) deux cas se présentent :
- S'il
s'agit d'un son périodique, on obtient un spectre discontinu ou spectre
de raies (seules certaines fréquences sont présentes dans le signal,
toutes les autres fréquences ont une intensité nulle).
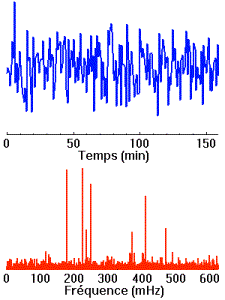
- S'il
s'agit d'un son apériodique, on obtient un spectre continu (toutes les
fréquences sont présentes dans le signal, à différentes intensités).
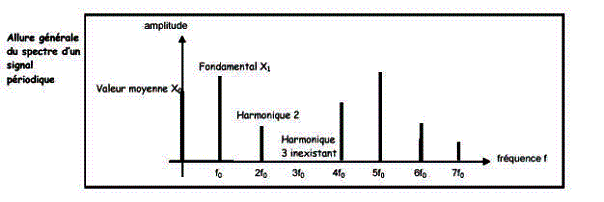
 Spectre
fréquentiel du son émis par la guitare.
Spectre
fréquentiel du son émis par la guitare.
On peut voir sur les figures ci-dessus que le spectre fréquentiel contient :
- le
niveau continu : valeur moyenne du signal
- la
composante fondamentale, de la fréquence du signal
- les
harmoniques,
de fréquences multiples de celle de la fondamentale
 Le
sonagraphe, dont la découverte remonte aux années 1940 dans les Bell
Laboratories, a permis d'explorer plus avant la décomposition du son en
harmoniques et d'autres composantes appelées partiels.
Le
sonagraphe, dont la découverte remonte aux années 1940 dans les Bell
Laboratories, a permis d'explorer plus avant la décomposition du son en
harmoniques et d'autres composantes appelées partiels.
En effet, un
son complexe est en réalité composé de plusieurs sons : un certain
nombre d'entre eux sont les harmoniques qui correspondent à des
multiples du son fondamental mais certains autres (ceux par exemple
obtenus en soufflant trop fort dans un tuyau) mais certains autres
appelés partiels correspondent à des fréquences différentes
quelconques.
Seul le sonagraphe,
appareil de représentation graphique de la totalité des dimensions
du phénomène (temps - fréquence - amplitude) a permis de suivre un
spectre évolutif, dont chaque composante a une intensité relative
qui évolue avec le temps.
L'inharmonicité définit
la nature d'un son musical dont les harmoniques ne sont pas des multiples
entiers du son fondamental.
En effet, si le cas du piano
ou même de la cloche sont caractéristiques de
l'inharmonicité, la plupart des instruments présentent une inharmonicité
relativement faible qui peut être négligée, mais jamais totalement nulle.
Dans un son inharmonique
les harmoniques sont généralement (voire toujours), plus hautes que les
multiples entiers du fondamental, et ce, d'autant plus que leur rang est élevé.
Cette caractéristique affecte le timbre du son, et se vérifie par l'examen
de son spectre harmonique. Ce phénomène peut donner l'illusion de
plusieurs hauteurs simultanées, comme pour la cloche.
 Retour à la page d'accueil
Retour à la page d'accueil
 Retour
au sommaire
Retour
au sommaire
 Retour
au plan détaillé
Retour
au plan détaillé
 Retour
au développement
Retour
au développement
 B)
Le son du piano - Timbre
B)
Le son du piano - Timbre
Un signal est dit périodique si les variations de son amplitude se reproduisent régulièrement au bout d'une période T constante comme sur la figure. Les instruments à cordes et à vent produisent ce type de signal sonore (les instruments à percussions produisant des signaux impulsionnels).
 Le mode propre dont la fréquence est la plus basse (n = 1) est
appelé mode fondamental : sa fréquence propre est notée f1.
Le mode propre dont la fréquence est la plus basse (n = 1) est
appelé mode fondamental : sa fréquence propre est notée f1.
 Dans le schéma ci-contre, l'onde jaune est la représentation du son
produit par une note quelconque, disons un La2.
Dans le schéma ci-contre, l'onde jaune est la représentation du son
produit par une note quelconque, disons un La2. Les premiers travaux de Joseph Fourier sur la décomposition d'une fonction
périodique de forme quelconque en une somme de fonctions sinusoïdales
simples avaient laissé penser que la différence entre deux sons de mêmes
fréquences et amplitudes devait se trouver dans l'analyse harmonique du
son.
Les premiers travaux de Joseph Fourier sur la décomposition d'une fonction
périodique de forme quelconque en une somme de fonctions sinusoïdales
simples avaient laissé penser que la différence entre deux sons de mêmes
fréquences et amplitudes devait se trouver dans l'analyse harmonique du
son.
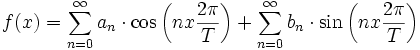
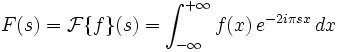


 Spectre
fréquentiel du son émis par la guitare.
Spectre
fréquentiel du son émis par la guitare. Le
sonagraphe, dont la découverte remonte aux années 1940 dans les Bell
Laboratories, a permis d'explorer plus avant la décomposition du son en
harmoniques et d'autres composantes appelées partiels.
Le
sonagraphe, dont la découverte remonte aux années 1940 dans les Bell
Laboratories, a permis d'explorer plus avant la décomposition du son en
harmoniques et d'autres composantes appelées partiels.